30.04.2025
3 minutes de lecture
Le climat évolue vite, trop vite. Les conséquences sur notre environnement sont déjà visibles dans de nombreuses régions du globe. Il est important dans ce contexte de comprendre la dynamique de notre environnement afin de construire des outils capables d’anticiper les risques qui découlent de cette perturbation climatique. Parmi ces outils, les modèles numériques offrent une solution très performante pour tester un grand ensemble de scénarios climatiques tout en considérant de nombreux processus physiques, chimique et biologiques.
Les modèles numériques d’évolution du paysage sont par exemple très utiles pour comprendre et quantifier la relation entre le climat et la dynamique hydro-sédimentaire d’un bassin versant. Deux ingrédients sont nécessaires à la construction d’un tel modèle : une « bonne louche » d’un modèle d’écoulement d’eau et une « grande tasse » de transport sédimentaire, le tout bien lié par une expertise associant géosciences et mathématiques appliquées ! C’est sur la base de cette recette que le logiciel Dionisos [1], devenu DionisosFlow [2], a été conçu pour modéliser les processus hydro-sédimentaires.
Un ingrédient de base : « la consistance numérique »
Un des points « sensibles » de ces modèles, connu depuis plus de 20 ans, est une dépendance à la taille et à la forme des mailles1 bien plus importante que celle que l’on peut habituellement imputer à la simple discrétisation numérique de nos équations continues. L’origine de cette dépendance est longtemps restée peu claire. En 2020, un premier article [2] venait identifier une des raisons pour lesquelles certains modèles d’écoulement d’eau utilisés classiquement par la communauté produisaient une dépendance artificielle à la maille. La raison était finalement simple : l’algorithme d’écoulement supposé mimer un modèle « empirique » était en réalité tout à fait reliable à une physique connue, à savoir un modèle de Manning-Strickler2. Or ces algorithmes n’avaient pas été explicitement conçus pour reproduire une physique connue, exprimable au travers d’un ensemble d’équations aux dérivées partielles. Et le hasard ne faisant pas tout le temps bien les choses, il se trouve qu’il manquait quelques ajustements dans ces algorithmes pour que cela soit le cas. Ces ajustements représentent ce que l’on appelle la « consistance numérique ». Sans elle, un algorithme est orphelin de sa physique : il modélise toujours quelque chose, mais quelque chose de complètement artificiel ! Ce défaut, présent dans les modèles historiques, est désormais corrigeable pour la plupart des algorithmes embarqués [3].
1 Un domaine numérique étant constitué d’un ensemble de mailles élémentaires
2 Formule empirique d’estimation de la vitesse moyenne d'un liquide s’écoulant en surface libre c’est-à-dire dans un conduit où le fluide ne remplit pas complètement la section ou dans un canal ouvert
Un ustensile indispensable : un filtre pour éliminer les grumeaux
Résoudre ce problème n’est cependant pas suffisant pour éviter les « grumeaux » (ces tous petits défauts dans la solution numérique qui, en s’amplifiant, viennent gâcher le plat !) dans les modèles d’évolution du paysage. En effet, l’autre aspect à prendre en compte est le couplage entre l’écoulement de l’eau et le transport des sédiments. Pour cela, nous nous sommes attachés à adapter une approche couramment déployée dans les modèles de type LES3 afin d’éliminer les « grumeaux » issus de la turbulence en deçà d’une certaine taille [4]. Concrètement, cela revient à ce que, d’une part, l’écoulement d’eau voie une topographie filtrée et à ce que, d’autre part, seuls des sédiments transportés par un réseau hydrique filtré impactent la topographie. L’ingrédient-clé est connu sous le nom de filtre de Leray-alpha4 : outre qu’il remplit la fonction recherchée, il a le bon goût de conserver les effets non-linéaires associés au couplage écoulement-transport, tout en filtrant les bruits numériques5.
3 Large Eddy Simulation : méthode de modélisation de la turbulence utilisée dans le domaine de la dynamique des fluides
4 Méthode de régularisation par moyenne locale de taille alpha
5 Erreurs dans la solution dues au processus de résolution numérique
Des résultats reproductibles d’une simulation à l’autre
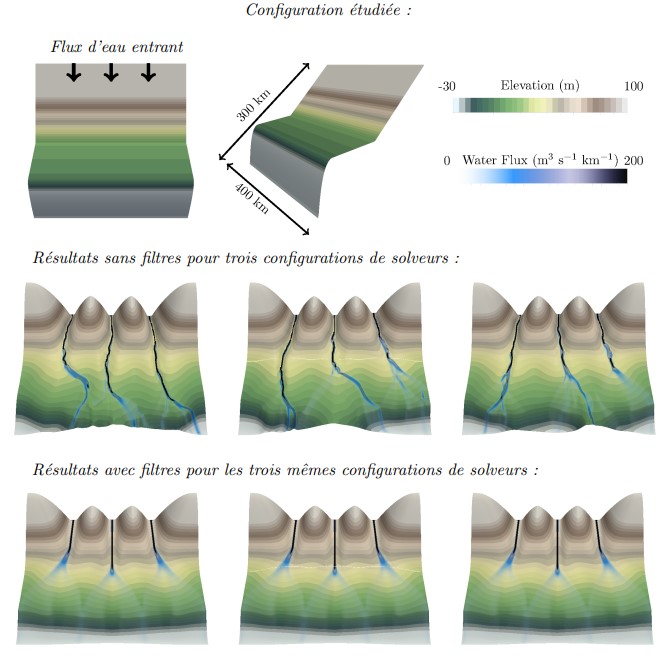
Le gain d’une telle méthode est apparu évident lorsque l’on a constaté qu’en son absence la reproductibilité des résultats n’était pas assurée. Cela se produisait par exemple lorsque, pour une même simulation, le problème était résolu avec des solveurs différents, ou même simplement lorsque on faisait varier le nombre de processeurs embarqués dans la résolution du système numérique. Les résultats obtenus étaient alors considérablement modifiés (une rivière, au lieu de couler tout droit, pouvait aléatoirement bifurquer) mais ceci est désormais résolu grâce à l’utilisation du filtre (Figure 1).
Des proportions bien respectées et le plat est prêt
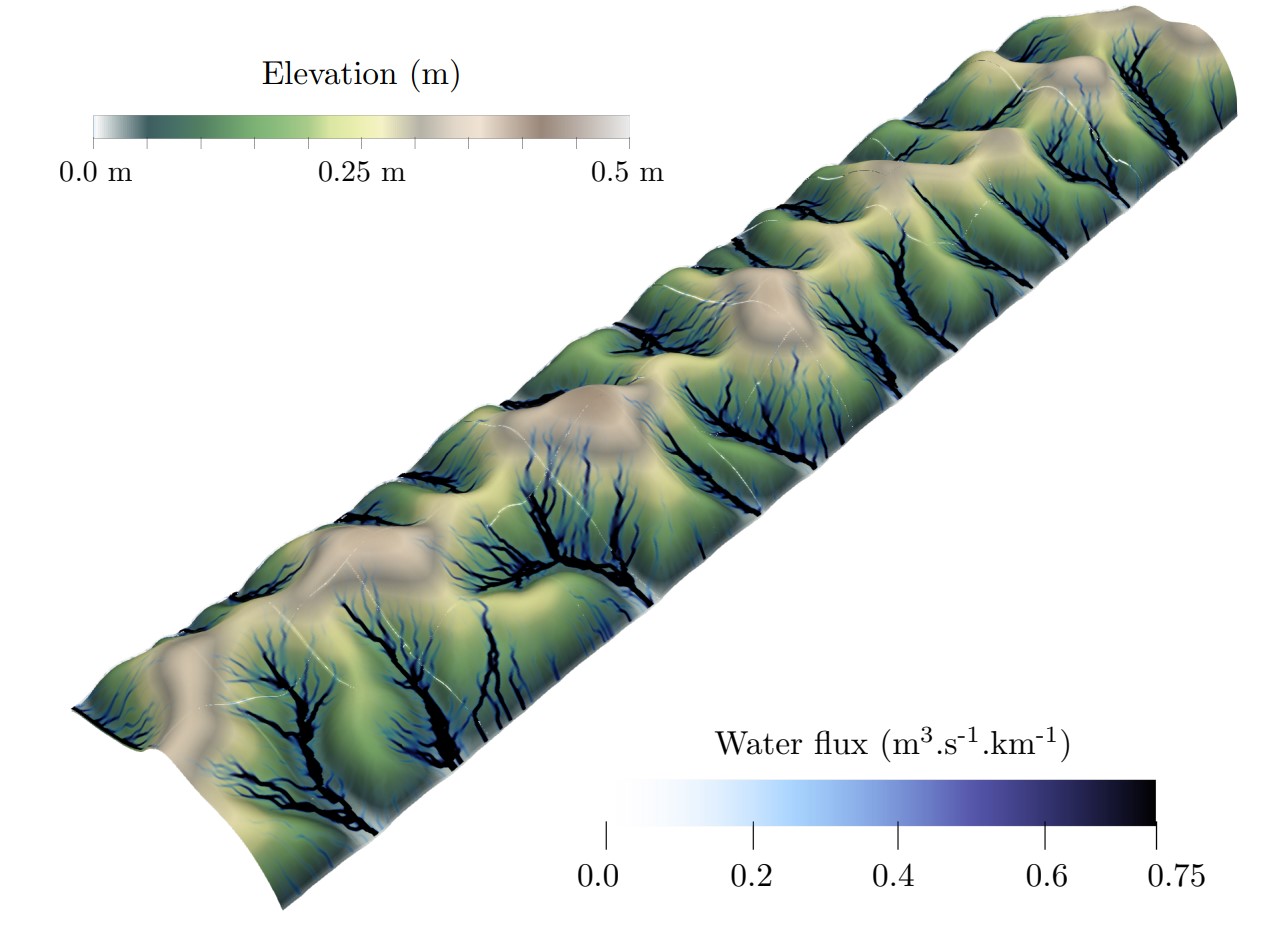
Comme pour toute bonne recette, il faut aussi respecter les proportions. Et c’est tout aussi vrai ici car la taille du filtre à choisir est conditionnée par celle des objets que l’on veut conserver dans notre paysage. A savoir qu’un objet de type montagne, bassin drainant ou même une simple rivière devrait être environ un ordre de grandeur supérieur à la taille du filtre. Une fois cette règle respectée, il ne reste plus qu’à adapter la taille de son maillage afin que celui-ci puisse « capturer » correctement le filtre et c’est prêt !(Figure 2)
Références :
[1] D. Granjeon (1996). Modélisation stratigraphique déterministe : Conception et applications d’un modèle diffusif 3-d multi-lithologique. PhD thesis, Université de Rennes I
[2] J. Coatléven (2020). Some multiple flow direction algorithms for overland flow on general meshes, ESAIM: Mathematical Modelling and Numerical Analysis.
>> DOI: https://doi.org/10.1051/m2an/2020025
[3] J. Coatléven; B. Chauveau (2025). A post-processing solution to restore numerical consistency for classical flow routing algorithms. Computational Geosciences
>> DOI : https://doi.org/10.1007/s10596-025-10359-5
[4] J. Coatléven; B. Chauveau (2024). Large structure simulation for landscape evolution models, Earth Surface Dynamics.
>> DOI: https://doi.org/10.5194/esurf-12-995-2024
Contacts scientifiques : Benoît Chauveau, Julien Coatléven
Vous serez aussi intéressé par
Connaissance et description des systèmes sédimentaires
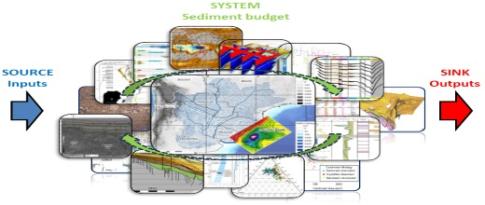
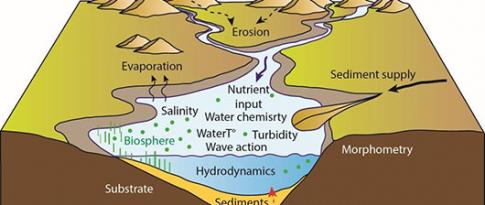
Budgets sédimentaires : concept, méthodes et intégration en analyse de bassin sur un continuum terre-mer Dans un compartiment sédimentaire donné, le budget sédimentaire consiste à évaluer les apports, les transferts et les exports sédimentaires, et à les assimiler au gain ou à la perte nette sur une unité de temps. Les budgets sédimentaires sont très largement utilisés en géosciences. Déployés à grande échelle, ils offrent la possibilité d’acquérir une vision globale des systèmes sédimentaires.
Changement global, impact sur les paysages et la ressource en eau
L’impact du changement climatique et des activités anthropiques sur l’évolution des paysages et des ressources en eau constitue aujourd’hui un enjeu majeur. Sa prévision nécessite de disposer d’outils dédiés capables d’évaluer à un horizon de 100 ans les conséquences de différents scénarios sur les bassins versants et les eaux souterraines. IFPEN développe à cette fin des approches de modélisation des phénomènes d’érosion-transport-dépôt couplés aux écoulements de surface et de subsurface...