Dans les procédés de transformation chimique mettant en œuvre une catalyse hétérogène, la phase active, qui accélère les transformations des molécules, est souvent déposée sur un support poreux. Celui-ci est doté d’une surface interne importante, permettant ainsi d’accueillir un grand nombre de sites actifs dans un faible volume. Ce support poreux est très souvent de l’alumine et doit à la fois avoir une tenue mécanique et une résistance thermique adéquates, et favoriser un transfert approprié de masse et de chaleur. Ces propriétés dépendent fortement de la texture du support, laquelle résulte du procédé de fabrication.
Pour les supports en alumine, ce procédé repose sur un phénomène de coagulation : l’assemblage de cristallites primaires de boehmitea (de 1 à 5 nm) forme des agrégats très stables (de 10 à 50 nm) qui constituent ensuite des agglomérats (de 100 nm à quelques dizaines de μm) [1]. En pratique, cette fabrication part d’une poudre de boehmite mélangée avec un acide, sous forme d’une pâte, afin de disperser les grains en petites particules d’agrégats, et ensuite avec une base pour déclencher la coagulation et former des agglomérats. Ce phénomène d’agglomération extrêmement chaotique implique un assemblage à plusieurs échelles de taille, de quelques dizaines de nanomètres à plusieurs microns qui détermine les propriétés finales du support.
Afin de modéliser la structure finale du support d’alumine en fonction des paramètres physicochimiques du milieu, un travail de thèseb s’est intéressé à la dynamique de l’agglomération en conditions statiques (absence de forces hydrodynamiques).
Pour quantifier l’impact du pH et de la force ionique, ainsi que de la concentration de boehmite, sur la cinétique d’agglomération, trois techniques expérimentales ont été utilisées : la diffusion dynamique de la lumière (DLS), la diffusion des rayons X aux petits angles (SAXS) et la microscopie électronique à transmission (STEM). Cette approche de caractérisation multi-techniques a permis de mettre en évidence les propriétés structurales à différentes échelles, informations qui ont été exploitées au travers de l’équation du bilan de population, alimentée par un modèle de dynamique Browniennec. Les résultats du bilan de population ont été ensuite utilisés pour paramétrer un modèle morphologique d’agglomération, capable de simuler la structure poreuse finale de l’alumine solide. Un jumeau numérique de la morphologie 3D d’un grain de boehmite après agglomération, au sein d’une suspension colloïdale, a ainsi été créé en prenant en compte des paramètres structuraux tels que la distribution de taille, la dimension fractaled et l’ordre d’assemblage.
La microstructure du solide final a été simulée en plusieurs étapes mettant en jeu successivement deux modèles physiques : un modèle de dynamique brownien lagrangien et un modèle de bilan de population.
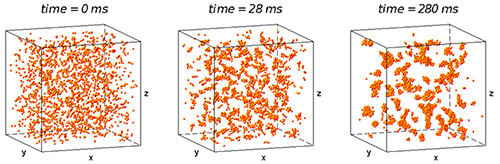
La première étape a consisté à bâtir un modèle morphologique d’agrégation de cristallites (figure 1). Différentes probabilités d’adhérence ont été attribuées aux points concaves et non concaves d’un agrégat, et reliées à des paramètres physico-chimiques. Le premier modèle a fourni des informations sur la relation entre la dimension fractale et la masse de l’agglomérat, propriété confirmée par les résultats de l’analyse SAXS [2].
Cette relation a ensuite été implémentée dans le modèle de bilan de population, permettant à celui-ci de simuler, de manière réaliste, un système colloïdal de grande taille. Les résultats expérimentaux de DLS ont été utilisés pour ajuster les paramètres du modèle.
Enfin, la distribution de taille et la dimension fractale obtenues à partir du bilan de population ont été utilisées pour paramétrer le modèle morphologique global et construire un agglomérat d’agrégats en 3D.
Le modèle morphologique développé intègre les conditions opératoires de génération d’une structure 3D adéquate et il pourra faire l’objet de nombreuses améliorations, telles que par exemple la prise en compte de particules non sphériques dans le modèle brownien. En considérant directement des cristallites de boehmite comme des particules primaires plutôt que leurs agrégats, il sera possible à terme de calculer les propriétés texturales du support d’alumine, telles que le volume poreux, la surface spécifique, la distribution des tailles de pores et la tortuosité. Une autre extension possible concernera la prise en compte du cisaillement à des concentrations en solide plus élevées, induisant des phénomènes d’agglomération forcée et de rupture, afin de pouvoir simuler le procédé de fabrication du support aluminique dans des conditions de fonctionnement industrielles.
a- Nom commun de l'oxyhydroxyde d'aluminium, oxyde naturel d'aluminium hydraté et constituant des bauxites.
b- Thèse de doctorat de G. Ferri : « Identification and study of relevant descriptors of the solid during the synthesis of boehmite », Université Paris-Saclay, 2021.
c- Méthode de simulation permettant de décrire la dynamique de particules en interaction dans un environnement qui amortit fortement leur mouvement.
d- Cette dimension caractérise la compacité de la structure d'un assemblage de particules. Sa valeur tend vers 1, 2 ou 3 respectivement pour les amas linéaires, planaires et sphériques. Les structures ouvertes ont une faible dimension fractale tandis que les structures compactes ont une dimension fractale élevée.
Références :
-
G. Ferri, S. Humbert, M. Digne, J-M. Schweitzer, M. Moreaud, Simulation of Large Aggregate Particles System with a New Morphological Model, Image Analysis & Stereology, 2021, vol. 40, pp 71-84.
>> https://www.ias-iss.org/ojs/IAS/article/view/2488
-
G. Ferri, S. Humbert, J-M. Schweitzer, M. Digne, V. Lefebvre, M. Moreaud, Mass fractal dimension from 2D microscopy images via an aggregation model with variable compactness, Journal of Microscopy, 2022, vol. 286, n° 1, pp 31-41.
>> DOI: https://doi.org/10.1111/jmi.13088
Contact scientifique : jan.verstraete@ifpen.fr





