Dans de nombreux réservoirs géologiques, la distribution de la taille des pores est très hétérogène (de 2 à 50 nm). Si la taille moléculaire des fluides confinés se situe entre 0,5 et 10 nm, leurs forces d'interaction avec la paroi des micropores (~2 nm) sont du même ordre de grandeur que leurs interactions intermoléculaires, ce qui peut modifier radicalement leur comportement thermodynamique. Comprendre ce phénomène présente un grand intérêt pour diverses industries : pétrolière, chimique, alimentaire, pharmaceutique, etc.
Cependant, obtenir expérimentalement les propriétés thermodynamiques requisesa reste techniquement difficile. La simulation moléculaire a été récemment employée à IFPEN pour modéliser des équilibres de phase dans des fluides confinés. Cette alternative permet de produire des données de référence pour les équations d’état utilisées dans la simulation des réservoirs.
Une nouvelle méthodologie de calcul Monte Carlob, avec une version modifiée de l’ensemble de Gibbs, a permis d’obtenir les propriétés thermodynamiques à l’équilibre des mélanges confinés et leurs pressions de liquide et de vapeur(1).
La méthode a été testée pour des hydrocarbures purs (C2, C5 et C10) et en mélange (C1/C2, C2/C5). Les pores ont été modélisés par des fentes avec des parois en graphite de différentes tailles. Les hydrocarbures l’ont été avec un potentiel d’atomes unifiés anisotropes, pour différentes proportions de mélange C2/C5 (figure). On observe que l'enveloppe de phase du fluide confiné est décalée et que sa taille se réduit. Les simulations confirment que la température et la pression critiques sont décalées vers le bas et que la pression au point de bulle diminue, alors que la pression au point de rosée augmente.
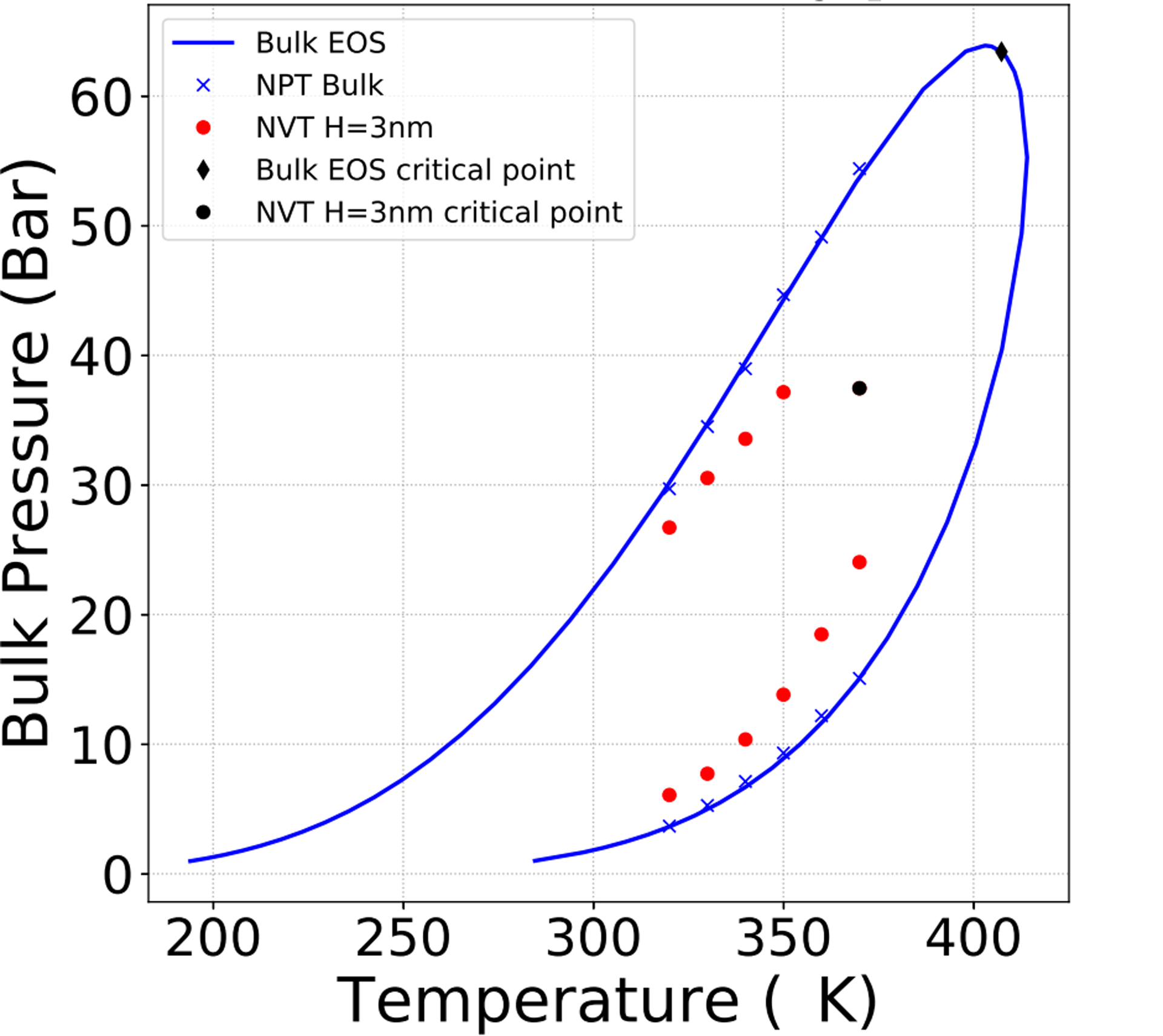
dans un nanopore de 3 nm c.
Ces informations vont permettre d’améliorer la description des fluides confinés par calibration des équations d’état.
a - Température critique, pression critique et masse volumique des phases.
b - Adaptation de la méthode en fixant la pression au point de bulle afin d’initialiser un calcul à température constante.
c - Les symboles représentent les résultats de simulation tandis que les lignes continues les résultats obtenus à partir d’une équation d’état cubique pour les fluides non confinés.
(1) N. Sobecki, C. Nieto-Draghi, A. Di Lella, D. Yu Ding. Phase behavior of hydrocarbons in nano-pores.
DOI.org/10.1016/j.fluid.2019.05.025
Contacts scientifiques : Carlos Nieto - didier.yu-ding@ifpen.fr





