Prix Yves Chauvin : Modélisation statistique des écoulements à phases dispersées avec inclusions fluides

Thèse de Nicolas Fintzi, lauréat du Prix Yves Chauvin 2025 : « Modélisation statistique des écoulements à phases dispersées avec inclusions fluides » 

Les écoulements de gouttes entraînées par la flottabilité constituent un type d’écoulement diphasique que l’on rencontre dans de nombreux procédés de génie chimique, tels que les séparateurs gravitaires, les extracteurs liquide-liquide ou encore les colonnes de flottation. La compréhension et la modélisation de ces écoulements sont essentielles, car elles permettent d’optimiser l’efficacité des procédés en question - par exemple en améliorant la séparation des phases et le transfert de matière.

Les systèmes physiques à modéliser couvrent une large gamme d’échelles, depuis la taille des gouttes (quelques micromètres) jusqu’à celle des réacteurs industriels (souvent supérieurs au mètre). Avec les ressources informatiques actuelles, la résolution complète de toutes ces échelles par simulation numérique demanderait un temps de calcul démesurément long.
C’est pourquoi, pour décrire l’évolution conjointe des phases dispersée (les gouttes) et continue (le fluide autour des gouttes), les approches modernes reposent sur l’utilisation d’équations moyennées. Ces équations décrivent les comportements moyens des deux phases sans nécessiter la résolution complète de tout l’écoulement aux échelles locales.

Par ailleurs, historiquement, la modélisation des écoulements diphasiques dispersés s’est principalement concentrée sur les suspensions de particules solides sphériques et, dans une moindre mesure, sur les émulsions, où la phase dispersée est fluide. Or, c’est cette dernière situation, lorsque la phase dispersée est constituée d’inclusions fluides, que l’on retrouve dans de nombreux contextes industriels ou naturels (écoulement à bulles, mélanges liquide-liquide, aérosols, etc).

L’objectif principal de cette thèse était la construction d’un ensemble d’équations moyennées capables de décrire des écoulements dispersés comportant des inclusions fluides. La phase dispersée y a été représentée par des lois de conservation lagrangiennes moyennées, tandis que la phase continue a été modélisée par des lois de conservation eulériennes moyennées (voir [1]). Un tel formalisme est donc appelé ''modèle hybride''.

Un second aspect de cette thèse a été le développement de modèles de fermeture permettant d’alimenter les équations du ''modèle hybride'' mis au point¹.

¹Ces ''modèles de fermeture'' permettent de représenter le comportement de l'écoulement aux échelles non résolues par les équations moyennées.

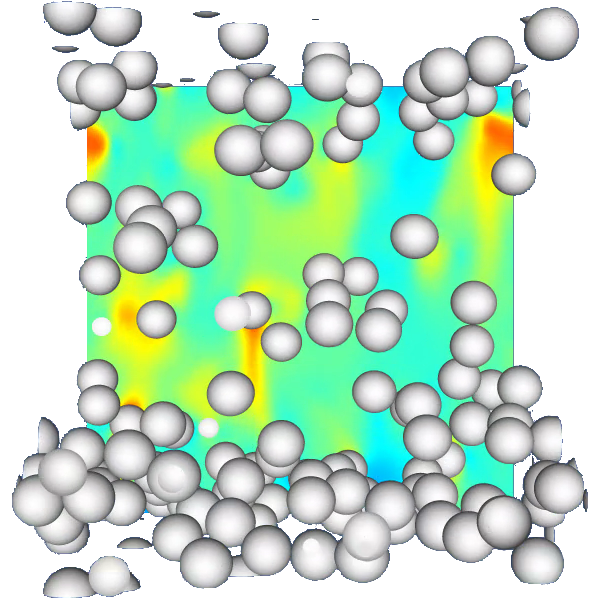
Nous avons ensuite utilisé le code open source « Basilisk C » pour réaliser des simulations numériques d’émulsions de gouttes soumises à la gravité (voir Figure 1), visant à prédire correctement leur comportement rhéologique [2].
Nos résultats, complétés par des analyses théoriques, montrent qu’il est essentiel d’inclure la contribution de la vitesse relative entre les phases, non seulement dans la force de traînée - force moyenne exercée par la phase continue sur les gouttes - mais également dans la contrainte effective², incluant les effets des fluctuations turbulentes.

² Contrainte observée à l’échelle macroscopique

Une dernière contribution de cette thèse concerne la caractérisation de la microstructure des émulsions et l’étude de la cinématique relative des gouttes en interaction. Pour cela, nous avons utilisé la fonction de distribution de paires des voisines les plus proches, qui décrit la probabilité de trouver une goutte à une certaine distance d’une autre.
Cette fonction a permis d’analyser la géométrie de la microstructure, autrement dit la manière dont les gouttes s’organisent dans l’espace.
Nous avons montré que l'écart type de cette distribution est un bon indicateur pour quantifier la formation d’amas, de chaînes ou de couches de gouttes dans l’écoulement [3].

Enfin, une équation décrivant l'évolution (dans le temps et dans l’espace) de l'écart type de cette distribution a été développée, permettant d’analyser la cinématique de la microstructure de l’émulsion. Nous avons montré que le temps moyen d’interaction entre gouttes correspond au temps de relaxation³ de l'écart-type de la distribution des paires les plus proches.
Ce temps caractéristique est donc un paramètre clé pour décrire la formation de la microstructure.

³ Durée nécessaire au retour à l’équilibre après la disparition d’une perturbation

Ce travail établit un cadre général solide pour de futures recherches sur les écoulements diphasiques dispersés, comme par exemple pour la prise en compte de la coalescence, de la déformation des gouttes ou de la turbulence induite par les amas de gouttes, autant de phénomènes qui sont encore mal maîtrisés et pourtant indispensables pour la modélisation des procédés. 

Références :

1. Fintzi, Nicolas, and Jean-Lou Pierson. "Averaged equations for disperse two-phase flow with interfacial transport."  (2024). (Accepted: International Journal of multiphase flows)
   >> arXiv preprint arXiv:2410.10752 
      
2. Fintzi, Nicolas, and Jean-Lou Pierson. " Averaged equations for suspensions made of slightly inertial buoyant spherical droplets." (en cours de soumission). 
         
3. Fintzi, Nicolas, Jean-Lou Pierson, and Stéphane Popinet. "Buoyancy driven motion of non-coalescing inertial drops: microstructure modeling with nearest particle statistics." Acta Mechanica (2024): 1-24.    
    

Contact scientifique : Nicolas Fintzi

>> NUMÉRO 59 DE SCIENCE@IFPEN